Tato elektronická podpora vznikla jako součást řešení grantového projektu FRVŠ 2421/2007/G1. Jedná se o projekt zaměřený na rozšíření výuky předmětu Vybrané matematické metody v mechanice o aktuální problematiku z oblasti lomové mechaniky heterogenních materiálů (obecných koncentrátorů) - viz Závěrečná zpráva projektu (PDF). Výstupem projektu jsou vstupní soubory do softwaru MAPLE 10, MATLAB 7.0 (a výš) a ANSYS 10.0 (a výš) a 4 komentované metodické listy, které mohou sloužit jako podklady do cvičení předmětu Vybrané matematické metody v mechanice. Veškerá potřebná teorie je uvedena v již zmíněné závěrečné zprávě a postupy užití zdrojových výpočtových souborů v příslušných metodických listech.

Všechny vstupní soubory seřazené do adresářů dle jednotlivých metodických listů lze stáhnout ZDE (formát ZIP):

• Adresář: 1_Singularita (včetně zdrojových souborů)
• Adresář: 2_GSIF (včetně zdrojových souborů)
• Adresář: 3_Premosteni (včetně zdrojových souborů)
• Adresář: 4_Kriteria (včetně zdrojových souborů)

Pozn.: Zabalený soubor modely.zip je třeba rozbalit do nějakého adresáře na libovolný pevný disk a dále se pro jejich další použítí řídit pokyny v jednotlivých metodických listech.

Veškeré dokumenty - závěrečná zpráva a jednotlivé metodické listy lze stáhnout ZDE (formát ZIP):

• Závěrečná zpráva - FRVS_Zaverecna zprava.pdf
• Metodický list č.0 - 0_Uvod.pdf
• Metodický list č.1 - 1_Analyza singularity.pdf
• Metodický list č.2 - 2_GSIF.pdf
• Metodický list č.3 - 3_Premosteni.pdf
• Metodický list č.4 - 2_Kriteria.pdf

Metodický list č. 1: (PDF)
Výpočet charakteristického vlastního čísla singularity (exponentu singularity napětí) pro obecný koncentrátor napětí.

Pro každý obecný koncentrátor (trhlina končící na rozhraní dvou různých materiálů, materiálový vrub, nebo jakýkoliv jiný více-materiálový klín) platí, že exponent singularity napětí je různý od 1/2. Je proto třeba mít k dispozici nástroj jak je stanovit.

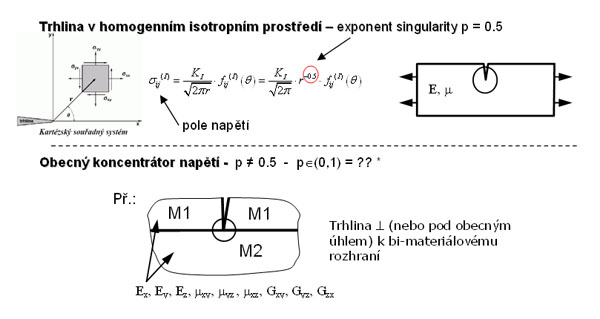
Tato úloha je zpracována v matematickém programu MAPLE jako vstupní soubor a detailně popsána v 1.metodickém listě a závěrečné zprávě. K výpočtu exponentu singularity a odpovídajících vlastních vektorů slouží vstupní soubor "Singularity analysis_orthotropic problem .mws" v adresáři "1_Singularita".

Metodický list č. 2: (PDF)
Výpočet zobecněného součinitele intensity napětí

Aby bylo možné popsat singulární složku pole napětí v asymptotickém rozvoji pro napětí, je třeba znát amplitudu této složky, tj. tzv. zobecněný součinitel intensity napětí (GSIF) - viz následujícící rovnice - veličina H:

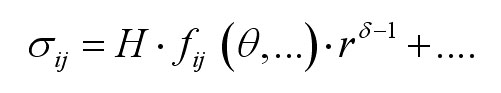
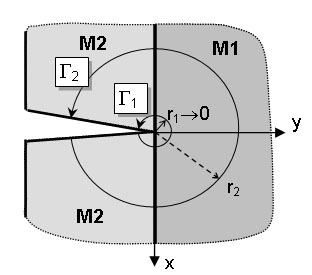
K výpočtu H byla zvolena metoda dvoustavového psí-integrálu, která umožňuje stanovit tuto veličinu z pole posuvů a deformací ve vzdálených místech od kořene trhliny, kde nejsou již výsledky MKP analýzy zatíženy chybou způsobenou přítomností singularity. K výpočtu GSIF slouží vstupní soubory do ANSYSu a MATLABu umístěné v adresáři "2_GSIF". Celá problematika výpočtu je opět popsána v závěrečné zprávě a konkrétní užití vstupních souborů v metodickém listě č.2 ve formátu PDF.

Metodický list č. 3: (PDF)
Zahrnutí vlivu přemostění trhliny do výsledného pole napětí - výpočet zobecněného mostícího součinitele intensity napětí.

Leží-li trhlina například v nějaké vrstvě laminátu složeného z vrstev vyztužených dlouhými vlákny, může nastat případ, kdy existující trhlina může být těmito vlákny přemostěna. V tomto případě mohou tato vlákna významně ovlivňovat výsledné pole napětí v okolí takovéto trhliny (může se významně lišit od nepřemostěného případu). Potom i další lomově-mechanické chování může být značně odlišné. Je proto důležité umět do výpočtu vliv vláken zahrnout.

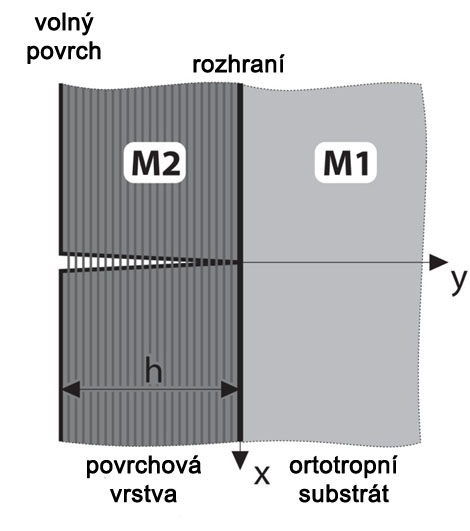
K výpočtu zobecněného mostícího součinitele slouží vstupní soubory do softwaru ANSYS a MATLAB umístěné v adresáři "3_Premosteni". Celá problematika výpočtu je opět popsána v závěrečné zprávě a konkrétní užití vstupních souborů v metodickém listě č.3 ve formátu PDF. Výstupem jsou grafické znázornění výsledného otevření trhliny s uvážením mostícího efektu při rostoucích zatěžovacích podmínkách a tyto grafické závislosti lze uložit také i jako animovaný výstup *.avi - viz následující ukázky:

Ukázkové výstupní video soubory:
- Jednoduchý Budinaského model přemostění
- Pokročilý statistický model přemostění

Metodický list č. 4: (PDF)
Odhad směru šíření trhliny končící na rozhraní dvou materiálů.

V této úloze je úkolem u zvolené materiálové konfigurace a daných zatěžovacích podmínek nalézt směr dalšího šíření trhliny. Trhlina končící na rozhraní se buď může šířit dále do materiálu M1 nebo se může odchýlit na rozhraní (viz následující obrázek). Delaminace podél rozhraní může mít obecně pozitivní vliv na další lomově mechanické chování konstrukce, jelikož se trhlina otupí a zmírní se tak její postup. Proto, má-li se trhlina šířit z rozhraní dál, tak ať je tomu tímto způsobem. Aby bylo možné daný koncentrátor napětí z tohoto hlediska posoudit, je třeba definovat nějaké lomové kriterium. Užito je kriterium založené na tzv. Konečné lomové mechanice a teorii sdružených asymptotických rozvojů.

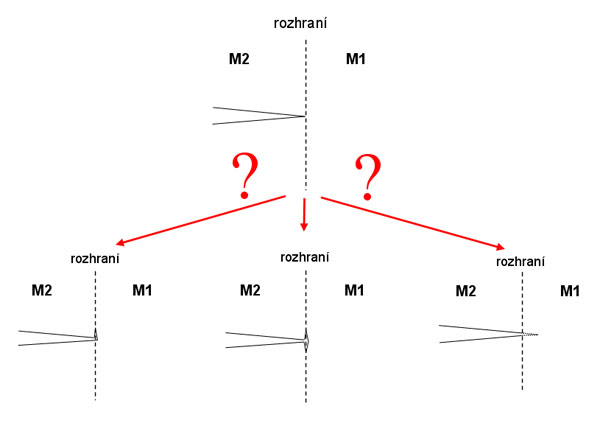
K řešení úlohy slouží vstupní soubory do systému ANSYS a MATLAB umístěné v adresáři "4_Kriteria" - popis jejich použití naleznete v metodickém listu č. 4 . Výstupem jsou výpočtené hodnoty změny potenciální energie pro jednotlivé případy (směry) šíření trhliny.